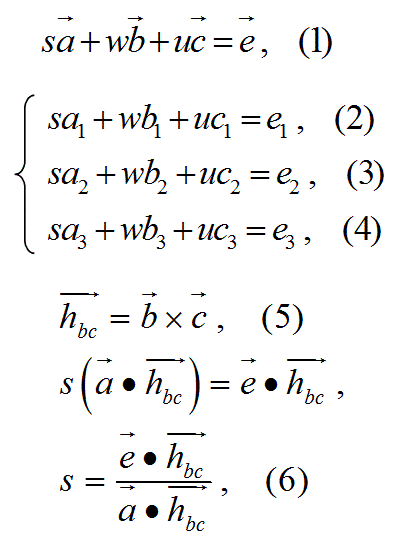【問】
実数a,bに関する条件p,qを次のように定める。
p: (a+b)2+(a-2b)2<5
q: (a+b)2<1 または (a-2b)2<4
次の①~④のうち、命題「q⇒p」に対する反例になっているのはどれか。
(反例候補)
①a=0,b=0
②a=1,b=0
③a=0,b=1
④a=1,b=1
【解答】
命題「q⇒p」に対する反例は、
q及び(pで無い)が成り立つ場合である。
(1)命題pとqをパラメータaとbであらわす式が複雑なので、命題の式の方をX、Yとおいて命題を見やすくする
(2)命題qが複雑なので、命題rとsの2つの命題に分けて、命題qを(rまたはs)に変換ずる。
r: (a+b)2<1
s: (a-2b)2<4
命題「q⇒p」に対する反例は、
(rまたはs)及び(pで無い)が成り立つ場合である。
この命題の範囲は、以下の式のように変換する。
(rまたはs)については、
(rまたは(s及び(rで無い)))
として、重なりが無い反例範囲に分ける。
そして、結局、反例範囲を、AとBとの2つに分ける。
(問題を簡単にする工夫)
このAとBとについて、別々に反例をさがす。
このAとBの反例範囲には、範囲の重なりが無いので反例探しに無駄が無い。
AとBとを別々に探すと、反例範囲の図は正確に書かないでも良く、図が簡単に手間がかからないようになる。
先ず、反例範囲Aに反例候補①②③④が入るかを調べる。
反例範囲を以下の図の斜線であらわす。
③の、a=0,b=1の場合は、
X=1なので、rを満足しない。よって反例では無い。
次に、反例範囲Bに反例候補①②③④が入るかを調べる。
③の、a=0,b=1の場合は、
Y=-2なので、sを満足しない。よって反例では無い。
④の、a=1,b=1の場合は、
X=2,Y=-1なので、sを満足する。
また、円周上の点なので、(pで無い)も満足する。
よって、④が反例である。
(解答おわり)
リンク:
高校数学の目次


【問】実数a,bに関する条件p,qを次のように定める。
p: (a+b)2+(a-2b)2<5
q: (a+b)2<1 または (a-2b)2<4
次の①~④のうち、命題「q⇒p」に対する反例になっているのはどれか。
①a=0,b=0
②a=1,b=0
③a=0,b=1
④a=1,b=1
【解答】
命題「q⇒p」に対する反例は、
q及び(pで無い)が成り立つ場合である。
命題pとqが複雑なので、命題の式の方をX、Yとおいて命題を見やすくし、
q及び(pで無い)が成り立つ場合を以下の図の斜線であらわす。
図の円周上の点は(pで無い)条件を満足している。
上図の斜線の範囲にある(X,Y)がq及び(pで無い)が成り立つ場合である。
とりあえず、XとYでbをあらわすと、
b=(X-Y)/3
である。
そのため、Y=Xの直線上の点はb=0を満たす点であることがわかる。
b=0でY=Xの直線上にある場合は、
a≧√(5/2)
あるいは、
a≦-√(5/2)
がなりたつべきであるが、
①と②はこの条件を満足していない。よって反例では無い。
あとは、③と④を個々に調べれば良い。
③の、a=0,b=1の場合は、
X=1,Y=-2なので、qを満足しない。よって反例では無い。
④の、a=1,b=1の場合は、
X=2,Y=-1なので、qを満足する。
また、円周上の点なので、(pで無い)も満足する。
よって、④が反例である。
(解答おわり)
リンク:
高校数学の目次


計算ミスを無くす方法
のサイトの助言がとても良いと思います。
このサイトでは、計算ミスを少なくするための1つとして、
とにかく計算方法をどんどん覚えること
を推薦してます。
的確なアドバイスと思います。
以下のよう三角形の外接円の中心Oと一辺BCとの作る二等辺三角形OBCの面積を求める問題を解いてみます。
最初の計算では、△OBC=2×△OBPとして計算します。
試験問題として答えは、(r・sinA)(r・cosA)までで十分で、これで解答が終わっています。
試験問題を解くときには時間が無いのでできないことですが、問題を解いたら、次のように進むのが、数学の心を捉えた良い数学の学び方と思います。
つまり、次に、その答えを、自分の知っている三角関数の倍角の公式を使ってsin(2A)の形に変形して結果がどうなるかを調べてみます。
そしてこの答えを見ることで、△OBCの面積は、辺OBと辺OCと、その間の角(2A)のsinとの積の2分の1であるとして直ぐ答えを計算できることが見出せます。
すなわち、最初の計算方法と、次に分かった計算方法との2つの計算方法があることがわかります。こうして自分が発見した(作った)計算の道の、その2つ目の解き方は自然に覚えられます。
こうして、1つ問題を解く毎に、新しい計算の道も作って、2つ以上の解き方を覚えていくことができます。
1問あたりに2倍の計算方法を覚えるので、確実に問題を解く力がついていきます。
このように問題を解いた後に、その問題を更に解析してもう1つの解き方まで発見する時間はとても大切なものです。
試験問題としてだけで問題を解くのは最低限度に留めて、
このように時間をかけて問題を何重にも解く時間をなるべく多く持つようにしましょう。
そうすれば、問題を解く計算の道が網の目のように張りめぐらされて、どの計算の道にも熟達します。
それにより、計算がつっかえて時間が足りなくなってあせるために起きる計算ミスを減らせます。
リンク:
高校数学の目次


計算ミスを無くす方法
のサイトの助言がとても良いと思います。
このサイトでは、計算ミスを少なくするための1つとして、
とにかく計算方法をどんどん覚えること
を推薦してます。
的確なアドバイスと思います。
以下のよう二等辺三角形の底辺の長さxを求める問題の解き方の道が4つあります。どの道を進んでも結局cosAが必要になります。
どの計算の道も最後まで通れるように、計算の道を覚えておきましょう。
そうすれば、計算がつっかえて時間が足りなくなってあせるために起きる計算ミスを減らせます。
必ず覚えるようにしたいですが、
数学センスに従う覚え方は、忘れる事を利用して、
以下の様に覚える事だと思います。
(1)先ず覚えて、次に、忘れて心の片隅に残す。
(2)この解き方が必要になった場面で、心の片隅からこの解き方がささやく心の声に従って、この公式を自分で導き出す。
(3)自分で導き出した公式は忘れない。本当に覚えるためには、最初は、忘れる事が必要だと思います。
(4)結論:
この解き方は、忘れられるようにし、次には、この解き方が必要になる場面に出会うため、問題を解く数学の勉強に多くの時間を使って数学に親しむ事に心がける。そうすれば心豊かに数学を学ぶことができると思います。
豊かに数学を学ぶため、覚えた事は忘れるように数学を学んで欲しい。
忘れる事を前提にして、十分な時間を数学とともに過ごす習慣をつけて欲しい。そのようにして忘れる事を受け入れて数学を学べば、数学とともに過ごす時間が楽しくなり、数学が人生を豊かにしてくれると思います。
リンク:
高校数学の目次


計算ミスを無くす方法
のサイトの助言がとても良いと思います。
このサイトでは、計算ミスを少なくするための1つとして、
とにかく計算方法をどんどん覚えること
を推薦してます。
的確なアドバイスと思います。
以下のように三角形の外接円の直径2rを計算する式を直ぐ思い出せるように、直径2rをあらわす形の式も覚えておきましょう。
そうすれば、計算がつっかえて時間が足りなくなってあせるために起きる計算ミスを減らせます。
必ず覚えるようにしましょう。
リンク:
高校数学の目次


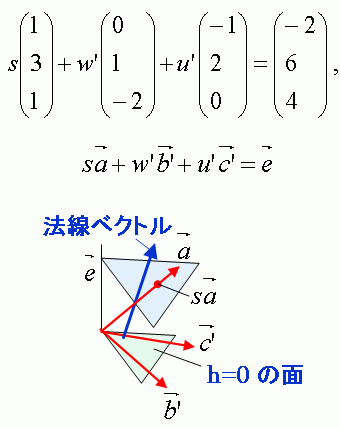
【問】以下の連立方程式を解いて未知数sを求めよ。
【解答】
連立方程式はベクトル方程式とみなして解くとやさしくなります。以下のようにベクトルの張る面に垂直な法線への射影を利用すると連立方程式の1つの未知数sを素早く求めることができます。
この式の水平面を張るベクトルbとcを、もっと使いやすいベクトルb’とc’に変更します(同時に未知数wとuも変わります)。
(ここで、水平面には変わりがありません)
このように、成分の1つを0にしたベクトルb’とc’で水平面を張ります。
このベクトル方程式を以下のようにして解きます。
(解答おわり)
① 先ず、問題の連立方程式の右辺のベクトルeのY成分のベクトルの高さを6zとしました。
② ベクトルbとcの張る面を水平面とする。ベクトルcのY成分の高さは①との関係で、高さ2zです。
③ ベクトルbのY成分の高さは①との関係で、高さzです。
④ ベクトルaのY成分の高さは①との関係で、高さ3zです。
⑤ ベクトルcは水平面上のベクトルなので、そのX成分はY成分による高さ2zを打ち消す高さ-2zです。
⑥ ベクトルeのX成分の高さは⑤との関係で、高さ-2z・2です。
⑦ ベクトルaのX成分の高さは⑤との関係で、高さ2zです。
⑧ ベクトルbは水平面上のベクトルなので、そのZ成分はY成分による高さzを打ち消す高さ-zです。
⑨ ベクトルeのZ成分の高さは⑧との関係で、高さ2zです。
⑩ ベクトルaのZ成分の高さは⑧との関係で、高さz/2です。
問題の連立方程式のsに掛かる高さは(⑦+④+⑩)であり、右辺の高さは(⑥+①+⑨)です。その比を計算してsが得られました。
【別解】ベクトルの外積を利用して計算すると、以下のように答えが得られます。
(解答おわり)
ベクトルの外積を利用する方が速そうです。
リンク:
高校数学の目次