

【問】以下の連立方程式を解いて未知数sを求めよ。
ページ内リンク
▷第1の解
▷第2の解
▷第3の解
▷第4の解
▷第5の解
【第1の解】
連立方程式はベクトル方程式とみなして解くとやさしくなります。以下のようにベクトルの張る面に垂直な法線への射影を利用すると連立方程式の1つの未知数sを素早く求めることができます。
(第1の解おわり)
① 先ず、問題の連立方程式の右辺のベクトルeのY成分のベクトルの高さを6zとしました。
② ベクトルbとcの張る面を水平面とする。ベクトルcのY成分の高さは①との関係で、高さzです。
③ ベクトルbのY成分の高さは①との関係で、高さ6zです。
④ ベクトルcは水平面上のベクトルなので、そのZ成分はY成分による高さzを打ち消す高さ-zです。
⑤ ベクトルbのZ成分の高さは④との関係で、高さ-z/2です。
⑥ ベクトルbは水平面上のベクトルなので、そのX成分はY成分とZ成分による高さを打ち消す高さ-11z/2です。
⑦ ベクトルaのX成分の高さは⑥との関係で、高さ(11z/2)(3/2)です。
問題の連立方程式のsに掛かる高さは⑦であり、右辺の高さは①です。その比を計算してsが得られました。
【第2の解】
ベクトルの外積を利用して計算すると、以下のように答えが得られます。
(第2の解おわり)
ベクトルの外積を利用する方が速そうです。
【第2の解(その2)】
第2の解の方法を、以下に整理して書きます。
なお、
である。
連立方程式2から4が解を持たない場合もあり得るが、それは、式6,9,10の分母が0になる場合に生じる。
(第2の解(その2)おわり)
【第3の解】
上記の第2の解とは異なる、以下の解き方で連立方程式を解く事もできます。
式15から17を使って以下の式18と19を導き出す。
この式18と19は、ベクトルzと内積計算した値が0になる、ベクトルzに垂直な2つのベクトルを表しています。
ベクトルzは、その2つのベクトルを外積したベクトルに平行である。
そのため、未知の係数kを使った以下の式20が得られる。
係数kは、式20と式15から得る式21で計算できる。
よって、ベクトルz=(s,w,u)が以下の式22で求められる。
この式22を変形して、以下の式23も得られる。
連立方程式15から17が解を持たない場合もあり得るが、それは、式23の分母が0になる場合に生じる。
(第3の解おわり)
なお、
である。
この式22及び式23の解は、第2の解(その2)の式6から式10の解とは異なる形で表された解ですが、同じ解をあらわしています。
【第4の解】
以下の解き方で連立方程式を解く事もできます。
これは、解が無い連立方程式が、その解が無いことが明確に分かる方法です。

の形をした、未知数s,t,uの連立方程式の問題を考える。具体的には以下の式を考える。

この連立方程式の各方程式の表す面の法線ベクトルは上記の通りである。各面の法線ベクトルが互いに垂直になるように、各面の方程式を変形する。


更に変形する。

このように、各面の法線ベクトルが互いに垂直になるように、各面の方程式を変形して上記の式を得た。そうすると、上記の式(7)によって、この方程式が解を持たないことが明らかに現れてきた。
(第4の解おわり)
【第5の解】
以下の解き方でも、解が無い連立方程式が、その解が無いことが明確に分かる。
以下の、未知数s,t,uの連立方程式を考える。

この連立方程式の拡大係数行列を以下に書く。

1行目-3(3行目):
2行目-4(3行目):

1行目/2:

2行目-3(1行目):

このように方程式を加減算する変形だけで、上記の式が得られる。その2行目の式によって、この方程式が解を持たないことが明らかに現れた。
(第5の解おわり)
リンク:
高校数学の目次
ページ内リンク
▷第1の解
▷第2の解
▷第3の解
▷第4の解
▷第5の解
【第1の解】
連立方程式はベクトル方程式とみなして解くとやさしくなります。以下のようにベクトルの張る面に垂直な法線への射影を利用すると連立方程式の1つの未知数sを素早く求めることができます。
(第1の解おわり)
① 先ず、問題の連立方程式の右辺のベクトルeのY成分のベクトルの高さを6zとしました。
② ベクトルbとcの張る面を水平面とする。ベクトルcのY成分の高さは①との関係で、高さzです。
③ ベクトルbのY成分の高さは①との関係で、高さ6zです。
④ ベクトルcは水平面上のベクトルなので、そのZ成分はY成分による高さzを打ち消す高さ-zです。
⑤ ベクトルbのZ成分の高さは④との関係で、高さ-z/2です。
⑥ ベクトルbは水平面上のベクトルなので、そのX成分はY成分とZ成分による高さを打ち消す高さ-11z/2です。
⑦ ベクトルaのX成分の高さは⑥との関係で、高さ(11z/2)(3/2)です。
問題の連立方程式のsに掛かる高さは⑦であり、右辺の高さは①です。その比を計算してsが得られました。
【第2の解】
ベクトルの外積を利用して計算すると、以下のように答えが得られます。
(第2の解おわり)
ベクトルの外積を利用する方が速そうです。
【第2の解(その2)】
第2の解の方法を、以下に整理して書きます。
である。
連立方程式2から4が解を持たない場合もあり得るが、それは、式6,9,10の分母が0になる場合に生じる。
(第2の解(その2)おわり)
【第3の解】
上記の第2の解とは異なる、以下の解き方で連立方程式を解く事もできます。
式15から17を使って以下の式18と19を導き出す。
この式18と19は、ベクトルzと内積計算した値が0になる、ベクトルzに垂直な2つのベクトルを表しています。
ベクトルzは、その2つのベクトルを外積したベクトルに平行である。
そのため、未知の係数kを使った以下の式20が得られる。
係数kは、式20と式15から得る式21で計算できる。
よって、ベクトルz=(s,w,u)が以下の式22で求められる。
この式22を変形して、以下の式23も得られる。
連立方程式15から17が解を持たない場合もあり得るが、それは、式23の分母が0になる場合に生じる。
(第3の解おわり)
なお、
である。
この式22及び式23の解は、第2の解(その2)の式6から式10の解とは異なる形で表された解ですが、同じ解をあらわしています。
【第4の解】
以下の解き方で連立方程式を解く事もできます。
これは、解が無い連立方程式が、その解が無いことが明確に分かる方法です。

の形をした、未知数s,t,uの連立方程式の問題を考える。具体的には以下の式を考える。

この連立方程式の各方程式の表す面の法線ベクトルは上記の通りである。各面の法線ベクトルが互いに垂直になるように、各面の方程式を変形する。


更に変形する。

このように、各面の法線ベクトルが互いに垂直になるように、各面の方程式を変形して上記の式を得た。そうすると、上記の式(7)によって、この方程式が解を持たないことが明らかに現れてきた。
(第4の解おわり)
【第5の解】
以下の解き方でも、解が無い連立方程式が、その解が無いことが明確に分かる。
以下の、未知数s,t,uの連立方程式を考える。

この連立方程式の拡大係数行列を以下に書く。

1行目-3(3行目):
2行目-4(3行目):

1行目/2:

2行目-3(1行目):

このように方程式を加減算する変形だけで、上記の式が得られる。その2行目の式によって、この方程式が解を持たないことが明らかに現れた。
(第5の解おわり)
リンク:
高校数学の目次




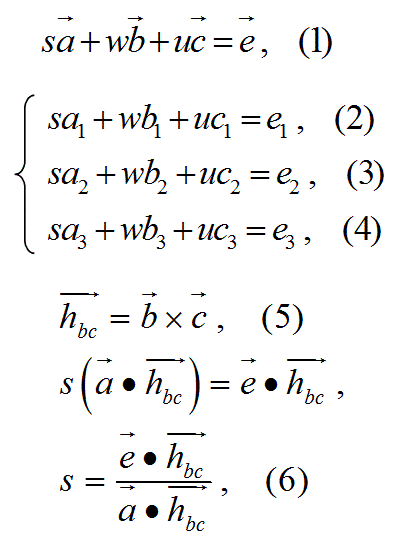








0 件のコメント:
コメントを投稿