

べクトルの内積を複素数を使って計算する
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式を覚えると、少しは計算が推進されます。
複素数平面であらわした複素数はベクトルです。
(実際、ベクトルPを複素数x+iyと等号で結ぶ表現をすることもあります。)

以下では、複素数平面上の複素数を用いてベクトルの内積の計算式をどの様に書けば良いかを、以下の問題を例にして説明します。
【問1】
複素数平面上で、原点0を中心にした半径Rの円がある。その円上の3点の座標を、複素数でα、β、γとすると、その3点が作る三角形の垂心の位置を表す複素数hは、
h=α+β+γ
で表わされる事を証明せよ。

【解答1】
h=α+β+γであらわされるとき、
もしhが垂心ならば内積が0になるベクトル(h-α)とベクトル(γ-β)の内積を、
以下の式で計算する。
(注意)
以上の計算では、複素数zとその共役複素数の差が2i・Im(z)になる公式を前提にして計算しました。大学入学試験レベルの問題に対してならば、その公式を前提にして計算を進めても良いだろうと考えます。
以上の計算の結果、ベクトル(h-α)とベクトル(γ-β)の内積は0になったので、
ベクトル(h-α)とベクトル(γ-β)は垂直である。
次に、同様にして、互いに垂直であるべきベクトル(h-β)とベクトル(γ-α)の内積を計算する。
以上の計算の結果、ベクトル(h-β)とベクトル(γ-α)の内積は0になったので、
ベクトル(h-β)とベクトル(γ-α)は垂直である。
以上の計算の結果、h=α+β+γは垂心である。
(証明終わり)
【解答2】
複素数平面の問題は、図形の問題にして考えると、解答が大幅に楽になります。以下では、そうして証明する例を示します。
頂点αから点Hまでのベクトル(h-α)を考える。
ベクトル(h-α)=ベクトル(β+ɤ)である。
そのベクトルは、図から分かるように、ベクトル(ɤ-β)に垂直である。
でその比を計算すると虚数になるので、両ベクトルが垂直である事がわかります。
同様にして、
ベクトル(h-β)=ベクトル(α+ɤ)⊥ベクトル(α-ɤ)
である。
よって、頂点Aや頂点Bから点Hまで引いたベクトルは、頂点Aや頂点Bに対向する辺に垂直である。
ゆえに、点Hは三角形ABCの垂心である。
(証明おわり)
【問2】
複素数平面上で、原点0を中心にした半径Rの円がある。その円上の3点の座標を、複素数でα、β、γとすると、その3点が作る三角形の垂心の位置を表す複素数hを求めよ。
【解答1】
複素数平面の問題は、図形の問題にして考えると、解答が大幅に楽になります。以下では、そうした解答の例を示します。
(解答おわり)
【解答2】
問題を簡単化するため、半径1の円に内接する三角形ABCを考えます。
その円の中心を複素数平面の原点Oにし、点A,B,Cの複素数平面での座標をα、β、ɤとします。
上図の、複素数であらわしたベクトルa,b,cを考えます。
ベクトルa=ɤ-β,
ベクトルb=α-ɤ,
ベクトルc=α-β,
です。
点Aから垂心Hまでのベクトルをあらわす複素数は、実数kのパラメータを使って:
ik(ベクトルa)
であらわせます。
すると、
ベクトルBHとベクトルbが垂直なので、両ベクトルの内積が0になる方程式を作れます。
その方程式を、以下の様に複素数を使って解く事ができます。

これで、実数のパラメータkの値が得られました。
これをik(ベクトルa)の式に代入して計算します。
ここで、計算を楽にするために、以下の、複素数平面の公式が必要になります。
(公式1)
2つの任意の単位ベクトルに関して、以下の公式が成り立ちます。
以下の計算によってこの公式を導き出すこともできます。

以下の式も成り立ちます。
この公式を使って、以下の計算をします。
この式を使って、ik(ベクトルa)の式の計算を続けます。
こうして、この公式1を使う事で、三角形の垂心の位置を表す複素数hをあらわす式を求める事ができました。
(解答おわり)
【問3】
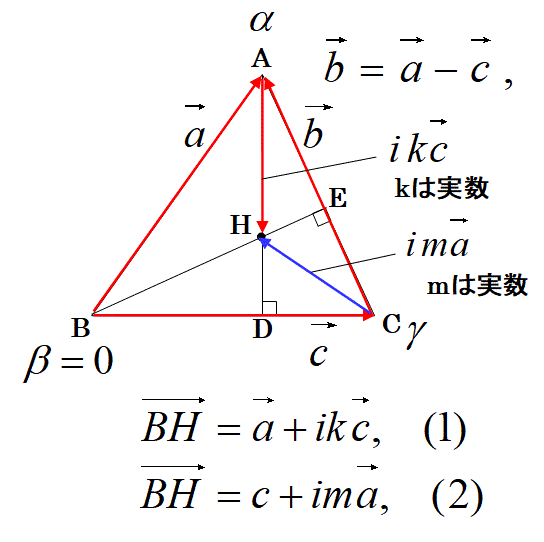
下図の三角形ABCの点Bが複素数平面の原点0にある場合に、垂心Hを複素数a=αと、複素数c=ɤであらわせ。
【解1】
(解答おわり)
【解2】
(解答おわり)
リンク:
高校数学の目次
複素数平面のベクトル方程式での垂心の導出
複素数平面で三角形の外心を求める
(第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
(優先順位の2位以下のこと)
それよりは優先順位が低いことですが、以下のような、複素数平面の計算の公式を覚えると、少しは計算が推進されます。
複素数平面であらわした複素数はベクトルです。
(実際、ベクトルPを複素数x+iyと等号で結ぶ表現をすることもあります。)

以下では、複素数平面上の複素数を用いてベクトルの内積の計算式をどの様に書けば良いかを、以下の問題を例にして説明します。
【問1】
複素数平面上で、原点0を中心にした半径Rの円がある。その円上の3点の座標を、複素数でα、β、γとすると、その3点が作る三角形の垂心の位置を表す複素数hは、
h=α+β+γ
で表わされる事を証明せよ。

【解答1】
h=α+β+γであらわされるとき、
もしhが垂心ならば内積が0になるベクトル(h-α)とベクトル(γ-β)の内積を、
以下の式で計算する。
(注意)
以上の計算では、複素数zとその共役複素数の差が2i・Im(z)になる公式を前提にして計算しました。大学入学試験レベルの問題に対してならば、その公式を前提にして計算を進めても良いだろうと考えます。
以上の計算の結果、ベクトル(h-α)とベクトル(γ-β)の内積は0になったので、
ベクトル(h-α)とベクトル(γ-β)は垂直である。
次に、同様にして、互いに垂直であるべきベクトル(h-β)とベクトル(γ-α)の内積を計算する。
以上の計算の結果、ベクトル(h-β)とベクトル(γ-α)の内積は0になったので、
ベクトル(h-β)とベクトル(γ-α)は垂直である。
以上の計算の結果、h=α+β+γは垂心である。
(証明終わり)
【解答2】
複素数平面の問題は、図形の問題にして考えると、解答が大幅に楽になります。以下では、そうして証明する例を示します。
頂点αから点Hまでのベクトル(h-α)を考える。
ベクトル(h-α)=ベクトル(β+ɤ)である。
そのベクトルは、図から分かるように、ベクトル(ɤ-β)に垂直である。
でその比を計算すると虚数になるので、両ベクトルが垂直である事がわかります。
同様にして、
ベクトル(h-β)=ベクトル(α+ɤ)⊥ベクトル(α-ɤ)
である。
よって、頂点Aや頂点Bから点Hまで引いたベクトルは、頂点Aや頂点Bに対向する辺に垂直である。
ゆえに、点Hは三角形ABCの垂心である。
(証明おわり)
【問2】
複素数平面上で、原点0を中心にした半径Rの円がある。その円上の3点の座標を、複素数でα、β、γとすると、その3点が作る三角形の垂心の位置を表す複素数hを求めよ。
【解答1】
複素数平面の問題は、図形の問題にして考えると、解答が大幅に楽になります。以下では、そうした解答の例を示します。
問題を簡単化するため、半径1の円に内接する三角形ABCを考えます。
その円の中心を複素数平面の原点Oにし、点A,B,Cの複素数平面での座標をα、β、ɤとします。
そして、その場合における垂心の位置ベクトルを複素数hであらわします。
ここで、上図の式のように、実数kと実数mの2つのパラメータ(2つの実数の未知数)を用いて、垂心の位置ベクトルの複素数hを表す2通りのベクトルの合成を等しいものと表したベクトル方程式を作ります。
その円の中心を複素数平面の原点Oにし、点A,B,Cの複素数平面での座標をα、β、ɤとします。
そして、その場合における垂心の位置ベクトルを複素数hであらわします。
ここで、上図の式のように、実数kと実数mの2つのパラメータ(2つの実数の未知数)を用いて、垂心の位置ベクトルの複素数hを表す2通りのベクトルの合成を等しいものと表したベクトル方程式を作ります。
(このベクトル方程式は、ベクトルで記述しても等価な式になります。)
垂心の複素数hを表す解の式は、点A,B,Cの複素数平面での座標のα、β、ɤに関して対称になると考えられます。
そのため、上の方程式から、α、β、ɤに関して対称な式
α+β+ɤ
を引き算する、方程式の変形を行ないます。

上の方程式の計算によって、実数のパラメータkとmの値が定まり、複素数hを表す式が求められた。垂心の複素数hを表す解の式は、点A,B,Cの複素数平面での座標のα、β、ɤに関して対称になると考えられます。
そのため、上の方程式から、α、β、ɤに関して対称な式
α+β+ɤ
を引き算する、方程式の変形を行ないます。

(解答おわり)
【解答2】
問題を簡単化するため、半径1の円に内接する三角形ABCを考えます。
その円の中心を複素数平面の原点Oにし、点A,B,Cの複素数平面での座標をα、β、ɤとします。
上図の、複素数であらわしたベクトルa,b,cを考えます。
ベクトルa=ɤ-β,
ベクトルb=α-ɤ,
ベクトルc=α-β,
です。
点Aから垂心Hまでのベクトルをあらわす複素数は、実数kのパラメータを使って:
ik(ベクトルa)
であらわせます。
すると、
ベクトルBHとベクトルbが垂直なので、両ベクトルの内積が0になる方程式を作れます。
その方程式を、以下の様に複素数を使って解く事ができます。

これで、実数のパラメータkの値が得られました。
これをik(ベクトルa)の式に代入して計算します。
ここで、計算を楽にするために、以下の、複素数平面の公式が必要になります。
(公式1)
2つの任意の単位ベクトルに関して、以下の公式が成り立ちます。
以下の計算によってこの公式を導き出すこともできます。

以下の式も成り立ちます。
この公式を使って、以下の計算をします。
この式を使って、ik(ベクトルa)の式の計算を続けます。
こうして、この公式1を使う事で、三角形の垂心の位置を表す複素数hをあらわす式を求める事ができました。
(解答おわり)
【問3】
下図の三角形ABCの点Bが複素数平面の原点0にある場合に、垂心Hを複素数a=αと、複素数c=ɤであらわせ。
【解1】
【解2】
(解答おわり)
リンク:
高校数学の目次
複素数平面のベクトル方程式での垂心の導出
複素数平面で三角形の外心を求める
















0 件のコメント:
コメントを投稿